Partition regularity
In mathematics, the notion of partition regularity in combinatorics is one approach to explaining when a set system is quite large.
Given a set  , a collection of subsets
, a collection of subsets 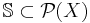 is called partition regular if every set A in the collection has the property that, no matter how A is partitioned into finitely many subsets, at least one of the subsets will also belong to the collection. That is, for any
is called partition regular if every set A in the collection has the property that, no matter how A is partitioned into finitely many subsets, at least one of the subsets will also belong to the collection. That is, for any 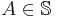 , and any finite partition
, and any finite partition 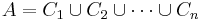 , there exists an i ≤ n, such that
, there exists an i ≤ n, such that 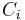 belongs to
belongs to 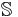 . Ramsey theory is sometimes characterized as the study of which collections
. Ramsey theory is sometimes characterized as the study of which collections 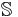 are partition regular.
are partition regular.
Examples
- the collection of all infinite subsets of an infinite set X is a prototypical example. In this case partition regularity asserts that every finite partition of an infinite set has an infinite cell (i.e. the infinite pigeonhole principle.)
- sets with positive upper density in
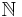 : the upper density
: the upper density 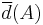 of
of  is defined as
is defined as 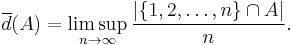
- For any ultrafilter
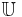 on a set
on a set  ,
, 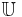 is partition regular. If
is partition regular. If 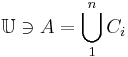 , then for exactly one
, then for exactly one  is
is 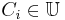 .
.
- sets of recurrence: a set R of integers is called a set of recurrence if for any measure preserving transformation
 of the probability space (Ω, β, μ) and
of the probability space (Ω, β, μ) and 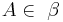 of positive measure there is a nonzero
of positive measure there is a nonzero 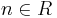 so that
so that 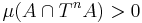 .
.
- Call a subset of natural numbers a.p.-rich if it contains arbitrarily long arithmetic progressions. Then the collection of a.p.-rich subsets is partition regular (Van der Waerden, 1927).
- Let
![[A]^n](/2012-wikipedia_en_all_nopic_01_2012/I/5fd0b09443f828c8ca7809689b6cc7e3.png) be the set of all n-subsets of
be the set of all n-subsets of  . Let
. Let ![\mathbb{S}^n = \bigcup^{ }_{A \subset \mathbb{N}} [A]^n](/2012-wikipedia_en_all_nopic_01_2012/I/fa88d2f3f638dd981fd85857a76a74bd.png) . For each n,
. For each n,  is partition regular. (Ramsey, 1930).
is partition regular. (Ramsey, 1930).
- For each infinite cardinal
 , the collection of stationary sets of
, the collection of stationary sets of  is partition regular. More is true: if
is partition regular. More is true: if  is stationary and
is stationary and  for some
for some  , then some
, then some  is stationary.
is stationary.
- the collection of
 -sets:
-sets:  is a
is a  -set if
-set if  contains the set of differences
contains the set of differences 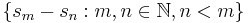 for some sequence
for some sequence 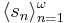 .
.
- the set of barriers on
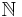 : call a collection
: call a collection 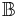 of finite subsets of
of finite subsets of 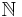 a barrier if:
a barrier if:
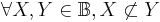 and
and- for all infinite
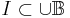 , there is some
, there is some 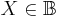 such that the elements of X are the smallest elements of I; i.e.
such that the elements of X are the smallest elements of I; i.e. 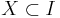 and
and 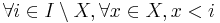 .
.
- This generalizes Ramsey's theorem, as each
![[A]^n](/2012-wikipedia_en_all_nopic_01_2012/I/5fd0b09443f828c8ca7809689b6cc7e3.png) is a barrier. (Nash-Williams, 1965)
is a barrier. (Nash-Williams, 1965)
- finite products of infinite trees (Halpern–Läuchli, 1966)
- piecewise syndetic sets (Brown, 1968)
- Call a subset of natural numbers i.p.-rich if it contains arbitrarily large finite sets together with all their finite sums. Then the collection of i.p.-rich subsets is partition regular (Folkman–Rado–Sanders, 1968).
- (m, p, c)-sets (Deuber, 1973)
- IP sets (Hindman, 1974, see also Hindman, Strauss, 1998)
- MTk sets for each k, i.e. k-tuples of finite sums (Milliken–Taylor, 1975)
- central sets; i.e. the members of any minimal idempotent in
 , the Stone–Čech compactification of the integers. (Furstenberg, 1981, see also Hindman, Strauss, 1998)
, the Stone–Čech compactification of the integers. (Furstenberg, 1981, see also Hindman, Strauss, 1998)
References
- Vitaly Bergelson, N. Hindman Partition regular structures contained in large sets are abundant J. Comb. Theory (Series A) 93 (2001), 18–36.
- T. Brown, An interesting combinatorial method in the theory of locally finite semigroups, Pacific J. Math. 36, no. 2 (1971), 285–289.
- W. Deuber, Mathematische Zeitschrift 133, (1973) 109–123
- N. Hindman, Finite sums from sequences within cells of a partition of N, J. Combinatorial Theory (Series A) 17 (1974) 1–11.
- C.St.J.A. Nash-Williams, On well-quasi-ordering transfinite sequences, Proc. Camb. Phil. Soc. 61 (1965), 33–39.
- N. Hindman, D. Strauss, Algebra in the Stone–Čech compactification, De Gruyter, 1998
- J.Sanders, A Generalization of Schur's Theorem, Doctoral Dissertation, Yale University, 1968.